1528. Подсчет общих подпоследовательностей

Подпоследовательность образуется из строки удалением нуля или нескольких символов из нее. По заданным трем строкам Вам следует подсчитать количество их разных непустых общих подпоследовательностей.

В примере 1 общими 6 подпоследовательностями будут: "c", "a", "l", "al", "ca" и "cl".

Вход. Каждый тест состоит из трех слов, которые находятся в трех разных строках. Длина каждого слова не более 50. Каждое слово состоит только из латинских букв нижнего регистра ('a' - 'z').

Выход. Для каждого теста вывести в отдельной строке количество разных непустых общих подпоследовательностей.

Пример входа	Пример выхода
call accelerate candle no correct answer	6 0

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

В ячейке f[i][j][k] будем хранить количество общих подпоследовательностей строк a₁a₂…a_i, b₁b₂…b_j и c₁c₂…c_k., где a_i = b_j = c_k. Если для тройки (i, j, k) последнее равенство не выполняется, то полагаем f[i][j][k] = 0. Если i = 0, то считаем, что строка a пустая. Аналогично при j = 0 (k = 0) считаем, что строка b (c) пустая. Положим f[0][0][0] = 1, считая, что общей подпоследовательностью трех пустых строк является пустая строка.

Искомое количество общих подпоследовательностей трех строк a, b и c равно

или – 1

где l, m, n – длины соответственно строк a, b и c.

Вычисление значений f[i][j][k] совершаем следующим образом. Перебираем все возможные значения троек (i, j, k) и для каждого значения f[i][j][k], большего нуля (a_i = b_j = c_k) перебираем все буквы латинского алфавита и для каждой буквы ищем ее появление во всех строках в позициях, больших соответственно i, j и k. Пусть такими позициями будут x, y и z. Добавляем к f[x+1][y+1][z+1] значение f[i][j][k] (индексы сдвинуты на 1, так как нумерация массивов в Си начинается с нуля, а индексу 0 в массиве f соответствует пустая строка).

Пример 1. Пусть a = b = c = “abc”. Тогда

f[0][0][0] = 1, общая подпоследовательность (“”, “”, “”).

f[1][1][1] = 1, общая подпоследовательность (“a”, “a”, “a”).

f[2][2][2] = 2, общие подпоследовательности (“b”, “b”, “b”), (“ab”, “ab”, “ab”).

f[3][3][3] = 4, общие подпоследовательности (“c”, “c”, “c”), (“bc”, “bc”, “bc”),

(“ac”, “ac”, “ac”), (“abc”, “abc”, “abc”).

Остальные значения f[i][j][k] равны нулю.

Количество общих подпоследовательностей равно 1 + 2 + 4 = 7.

Пример 2. Пусть a = “abcda”, b = “bakca”, c = “dlaca”.

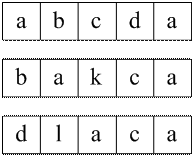
Положим f[0][0][0] = 1. Это значение будет добавлено в:

f[1][2][3] по букве 'a' (“a”, “a”, “a”)

f[3][4][4] по букве 'c' (“c”, “c”, “c”)

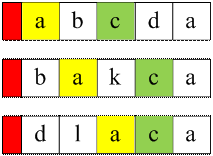
Значение f[1][2][3] = 1 будет добавлено в:

f[3][4][4] по букве 'c' (“ac”, “ac”, “ac”), (“c”, “c”, “c”)

f[5][5][5] по букве 'a' (“aa”, “aa”, “aa”)

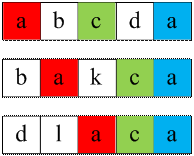
Значение f[3][4][4] = 2 будет добавлено в:

f[5][5][5] по букве 'a' (“aca”, “aca”, “aca”), (“ca”, “ca”, “ca”), (“aa”, “aa”, “aa”)

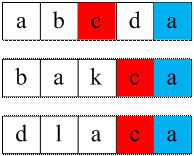
По окончанию работы алгоритма ненулевыми (кроме f[0][0][0]) будут следующие значения массива f:

f[1][2][3] = 1 (“a”, “a”, “a”),

f[3][4][4] = 2 (“ac”, “ac”, “ac”), (“c”, “c”, “c”),

f[5][5][5] = 3 (“aca”, “aca”, “aca”), (“ca”, “ca”, “ca”), (“aa”, “aa”, “aa”)

Количество общих подпоследовательностей равно 1 + 2 + 3 = 6. Все они перечислены выше.

Реализация алгоритма

Объявим трехмерный массив f и символьные массивы s1, s2, s3, в которых будем хранить входные строки.

long long f[51][51][51], res;

char s1[100], s2[100], s3[100];

Функция countCommonSubsequences вычисляет количество разных непустых общих подпоследовательностей в строках a, b, c.

long long countCommonSubsequences(string a, string b, string c)

{

int i, j, k, x, y, z;

f[0][0][0] = 1; res = 0;

for(i = 0; i <= a.size(); i++)

for(j = 0; j <= b.size(); j++)

for(k = 0; k <= c.size(); k++)

if (f[i][j][k] > 0)

{

for(char ch = 'a'; ch <= 'z';ch++)

{

x = a.find(ch,i); y = b.find(ch,j); z = c.find(ch,k);

if (x != string::npos && y != string::npos &&

z != string::npos)

f[x+1][y+1][z+1] += f[i][j][k];

}

res += f[i][j][k];

}

return res - 1;

}

Основная часть программы.

while(gets(s1))

{

gets(s2);gets(s3);

memset(f,0,sizeof(f));

long long res = countCommonSubsequences(s1,s2,s3);

printf("%lld\n",res);

}